| Concursos |

CESGRANRIO 2025 – BANESE – Técnico Bancário – Sequência – Questão Resolvida

Uma sequência numérica é tal que seus termos a_1= a_2 = 1 e a_{n+2} = a_{n+1} -a_n , para todo n \geq 1.
O termo a_{35} dessa sequência é igual a
(A) -35
(B) -1
(C) 0
(D) 1
(E) 35

RESOLUÇÃO

Temos uma sequência recursiva onde cada termo, a partir do terceiro, é a diferença entre o termo anterior e o anterior do anterior.

Em geral, nesse tipo de questão, não precisamos construir a sequência completa e sim perceber se algum padrão irá se formar a partir dos primeiros termos.

a_1 = 1
a_2 = 1
a_3 = a_2 - a_1 = 1 - 1 = 0
a_4 = a_3 - a_2 = 0 - 1 = -1
a_5 = a_4 - a_3 = -1-0 = -1
a_6 = a_5 - a_4 = -1-(-1) = -1+1=0
a_7 = a_6 - a_5 = 0-(-1) = 0+1=1
a_8 = a_7 - a_6 = 1-0 =1

Note que os termos a_7 = a_8 = 1 repetem a situação inicial, onde tínhamos a_1 = a_2 = 1. Ou seja, a sequência começa a se repetir em um ciclo de tamanho 6.

(a_1,a_2,a_3,a_4,a_5,a_6) = (1,1,0,-1,-1,0)
(a_7,a_8,a_9,a_{10},a_{11},a_{12}) = (1,1,0,-1,-1,0)

Quando temos uma situação desse tipo, podemos encontrar um termo qualquer pela observação do resto da divisão inteira da posição do termo pelo tamanho do ciclo (6).

\text{Resto } 1 \to a_1
\text{Resto } 2 \to a_2
\text{Resto } 3 \to a_3
\text{Resto } 4 \to a_4
\text{Resto } 5 \to a_5
\text{Resto } 0 \to a_6

Para obtermos o termo a_{35} dividimos 35 por 6.

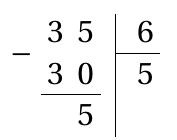
Como podemos observar 35 \div 6 =5 \text{ (quociente)} com resto \fbox{5} , dessa forma, temos a_{35} = a_5 = \fbox{-1}

✅ Resposta correta: (B) -1

O que você achou da resolução dessa questão de SEQUÊNCIAS e ARITMÉTICA MODULAR da banca CESGRANRIO? Deixe o seu comentário e faça sugestões de questões e provas que você gostaria de ver resolvidas aqui no site!



Deixe um comentário