FMJ, Vestibular

Faculdade de Medicina de Jundiaí 2025 – Média, Moda e Mediana

QUESTÃO 11
O gráfico mostra informações sobre o número de alunos que foram aprovados em um curso de Estatística em seis classes do terceiro ano do ensino médio de uma escola, sendo que as informações a respeito do 3º F não saíram nítidas.

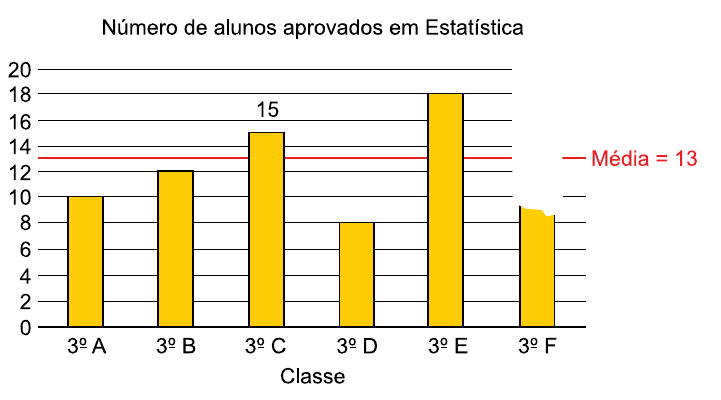
De acordo com as informações disponíveis no gráfico, a razão entre a mediana e a moda do número de alunos aprovados em Estatística das seis classes, nessa ordem, é igual a:
(A) 27/20
(B) 9/8
(C) 3/4
(D) 9/10
(E) 27/16

Resolução:

Primeiro vamos obter o número de alunos aprovados no 3ºF.

$\dfrac{10 + 12 + 15 + 8 + 18 + F}{6} = 13$

$63 + F = 6 \cdot 13$

$F = 78 -63$

$F = 15$

Ordenando os dados, temos:

8,10,12,15,15,18

A mediana é a média aritmética dos dois valores centrais:

$Me = \dfrac{12 + 15}{2} = \dfrac{27}{2} = 13,5$

A moda é o valor de maior frequência, no caso temos: $Mo = 15$

Como queremos a razão entre a mediana e a moda, teremos:

$\dfrac{13,5}{15} = \dfrac{13,5\cdot 2}{15 \cdot 2} = \dfrac{27}{30}$

$\dfrac{27 \div 3}{30 \div3} = \dfrac{9}{10}$

Alternativa (D)

📘 Quer ver mais questões como esta resolvidas em vídeo?
Na Apostila gratuita de Matemática para Vestibulares você encontra esta e muitas outras questões organizadas por prova, com links para as resoluções em vídeo.

👉 Clique aqui e acesse gratuitamente Apostila de Matemática para Vestibulares

Deixe um comentário Cancelar resposta