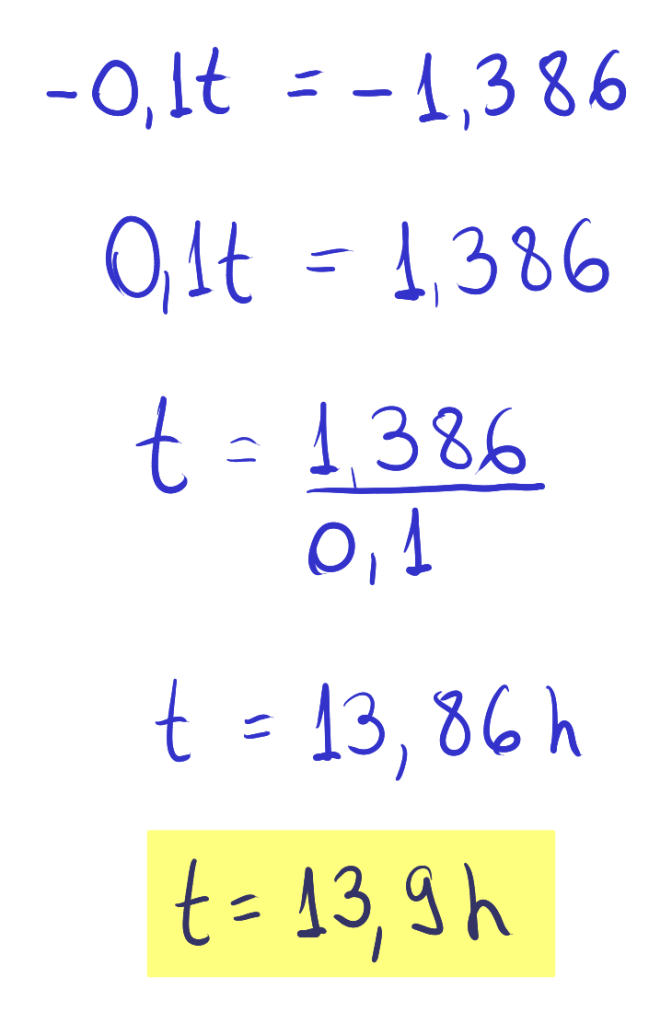QUESTÃO 60 Um médico está monitorando a concentração de um medicamento no sangue de seu paciente para ajustar a próxima dosagem. Essa concentração segue o modelo de decaimento exponencial descrito pela fórmula:

Em que:

• é a concentração inicial do medicamento,em mg/L.
• k é a constante de eliminação do medicamento, em .
• t é o tempo em horas.

Sabe-se que a constante de eliminação k do medicamento é 0, 1h −1 . O médico administrou uma dose inicial que resultou em uma concentração inicial de 100 mg/L. Para garantir que o medicamento permaneça eficaz, o médico precisa calcular quanto tempo levará para que a concentração do medicamento no sangue do paciente caia para 25 mg/L.
Qual é o valor aproximado de t necessário para que a concentração do medicamento no sangue seja reduzida para 25 mg/L?
Considere ln(100) = 4,6 e ln(0, 25) = −1,386
(A) 13,9 horas.
(B) 16,1 horas.
(C) 19,3 horas.
(D) 20,2 horas.
(E) 24,5 horas.

📘 Quer ver mais questões como esta resolvidas em vídeo?
Na Apostila gratuita de Matemática para Vestibulares você encontra esta e muitas outras questões organizadas por prova, com links para as resoluções em vídeo.