QUESTÃO 20
No plano cartesiano, a reta s corta o eixo y no ponto de ordenada – 2 e é paralela à reta r, cuja equação reduzida é , como mostra a figura.

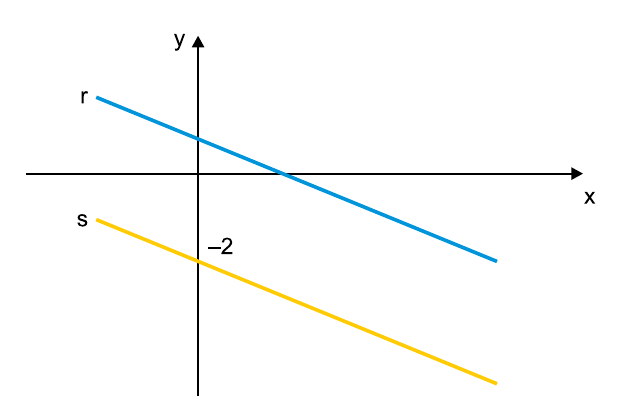
A equação reduzida da reta s é:
(A)

(B)

(C)

(D)

(E)

Para resolver essa questão de geometria analítica, o objetivo é encontrar a equação reduzida da reta s. A forma geral da equação reduzida é y = ax + b, onde “a” é o coeficiente angular e “b” é o coeficiente linear.
A estratégia é usar as duas informações fornecidas no enunciado para determinar os valores de “a” e “b” para a reta s.
Encontrar o coeficiente linear (b): O enunciado afirma que a reta s corta o eixo Y no ponto de ordenada -2. Por definição, o coeficiente linear “b” é exatamente o ponto onde a reta intercepta o eixo Y. Portanto, já sabemos o valor de “b”.
Encontrar o coeficiente angular (a): O enunciado diz que as retas r e s são paralelas. Uma propriedade fundamental de retas paralelas é que elas possuem o mesmo coeficiente angular. Observando a equação da reta r (y = -2/5x + 3/5), podemos identificar diretamente o seu coeficiente angular. Esse será também o valor de “a” para a nossa reta s.
Com os valores de “a” e “b” em mãos, basta montar a equação y = ax + b para encontrar a resposta.
Assista ao vídeo acima para ver a identificação direta dos coeficientes “a” e “b” e a montagem da equação final.

📘 Quer ver mais questões como esta resolvidas em vídeo?
Na Apostila gratuita de Matemática para Vestibulares você encontra esta e muitas outras questões organizadas por prova, com links para as resoluções em vídeo.