QUESTÃO 14
No plano cartesiano, a partir de A(0, 0) e B(4, 0) foi construído um quadrado ABCD, um quadrado BDFE e um quadrado BFGH.
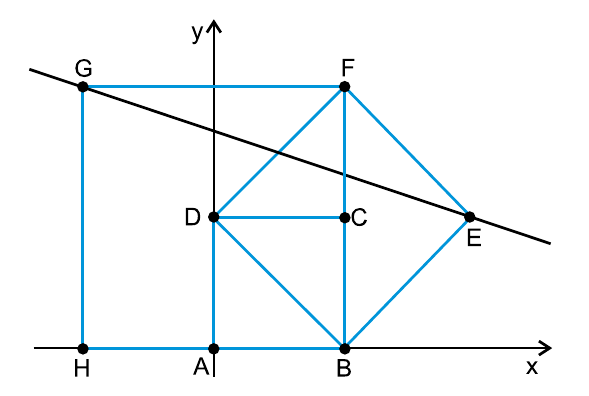
A equação da reta EG é
(A) x + 3y – 20 = 0
(B) x + 4y – 16 = 0
(C) x + 4y – 20 = 0
(D) x + 3y – 16 = 0
(E) x + 3y – 24 = 0
Para resolver essa questão, o objetivo é descobrir a equação da reta que passa pelos pontos E e G. A estratégia principal é, primeiro, determinar as coordenadas exatas desses dois pontos.
Analisando a construção dos quadrados a partir dos pontos A(0,0) e B(4,0), podemos deduzir as dimensões e posições das figuras. O primeiro quadrado, ABCD, tem lado 4. Isso nos ajuda a encontrar as coordenadas dos pontos C e D.
Em seguida, usamos as propriedades dos quadrados e suas diagonais para encontrar as coordenadas dos pontos F, E, e G. Por exemplo, o cruzamento das diagonais de um quadrado ocorre em seu ponto médio, o que é uma informação crucial para descobrir a posição de E. Da mesma forma, sabendo o lado do quadrado BFGH, podemos determinar a abscissa e a ordenada de G.
Uma vez que temos as coordenadas dos pontos E e G, podemos usar o método do determinante para encontrar a equação geral da reta. O cálculo envolve o mesmo conceito de montar uma matriz 3×3 com (x, y), as coordenadas de E e as coordenadas de G, e igualar seu determinante a zero, porém de uma forma simplificada.
Assista ao vídeo acima para ver a dedução detalhada de cada coordenada, a aplicação do cálculo do determinante e como chegar à equação final da reta EG.
Matemática para Vestibulares 