QUESTÃO 15
No plano, um lado de um retângulo está sobre a reta r. Um ponto P, sobre a reta r, é tal que o segmento de reta que liga P a um dos vértices do retângulo forma, com um de seus lados, um ângulo α, conforme mostra a figura.

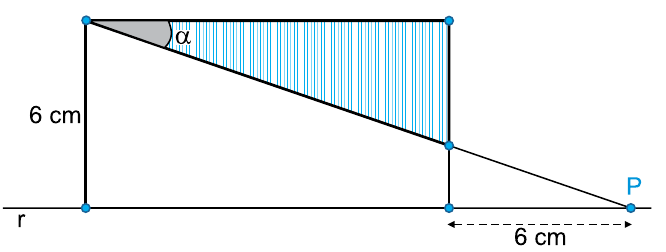
Sabendo que tg α = 1/3, a área do triângulo hachurado na figura é
(A) 30 cm².
(B) 21 cm².
(C) 24 cm².
(D) 27 cm².
(E) 18 cm².

Para resolver essa questão, o objetivo é calcular a área do triângulo hachurado. Como é um triângulo retângulo, sua área é dada por (base x altura) / 2. Vou chamar a base de X e a altura de Y.

A informação principal fornecida é que a tangente do ângulo α é igual a 1/3. A chave da resolução está em identificar dois triângulos retângulos diferentes na figura onde podemos aplicar essa relação.

O primeiro é o triângulo maior, que inclui o retângulo. Nesse triângulo, o cateto oposto a α mede 6, e o cateto adjacente é a soma do lado do retângulo (6) com a base do nosso triângulo (X). Montando a relação da tangente (cateto oposto / cateto adjacente) e igualando a 1/3, conseguimos encontrar o valor de X.

O segundo triângulo é o próprio triângulo hachurado. Nele, o cateto oposto a α é Y e o cateto adjacente é X. Usando novamente a relação da tangente e o valor de X que acabamos de encontrar, podemos calcular o valor de Y.

Com os valores de X e Y em mãos, basta aplicar a fórmula da área do triângulo.

Assista ao vídeo acima para ver a aplicação detalhada da tangente em ambos os triângulos, os cálculos para encontrar X e Y, e a determinação da área final.

📘 Quer ver mais questões como esta resolvidas em vídeo?
Na Apostila gratuita de Matemática para Vestibulares você encontra esta e muitas outras questões organizadas por prova, com links para as resoluções em vídeo.