QUESTÃO 16
Um sólido foi construído a partir de quatro paralelepípedos reto-retângulos, sólidos e idênticos, com alguns vértices em comum e algumas faces sobrepostas, conforme mostra a figura.
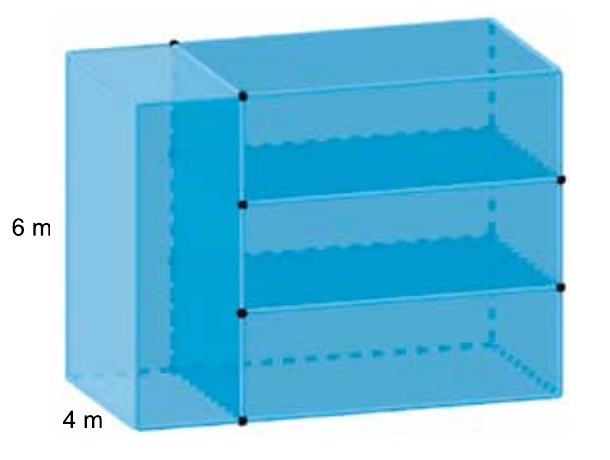
O volume ocupado por esses 4 paralelepípedos é igual a
(A) 200 m³.
(B) 208 m³.
(C) 216 m³.
(D) 192 m³.
(E) 180 m³.
Para resolver essa questão, o objetivo é calcular o volume total do sólido, que é composto por quatro paralelepípedos idênticos. A estratégia mais direta é calcular o volume de um único paralelepípedo e, em seguida, multiplicar esse resultado por quatro.
Analisando a figura, podemos focar em um dos paralelepípedos para determinar suas três dimensões: comprimento, largura e altura. Duas dessas dimensões são dadas diretamente na figura como 6 metros e 4 metros.
A terceira dimensão, que corresponde à “espessura” de cada bloco, não é informada diretamente, mas pode ser deduzida. Observando a parte superior do sólido, vemos que a dimensão de 6 metros é composta pela sobreposição de três dessas espessuras. A partir dessa informação, podemos calcular o valor dessa dimensão faltante.
Uma vez que as três dimensões de um paralelepípedo são conhecidas, calculamos seu volume multiplicando-as. O passo final é multiplicar esse volume individual por quatro para obter o volume total do sólido.
Assista ao vídeo acima para ver a dedução da dimensão que falta e o cálculo completo para chegar ao volume final.