QUESTÃO 16
No plano cartesiano de origem O, a reta r, de equação , corta o eixo x no ponto P e o eixo y no ponto Q. A reta s passa pela origem e encontra a reta r no ponto R, conforme mostra a figura.

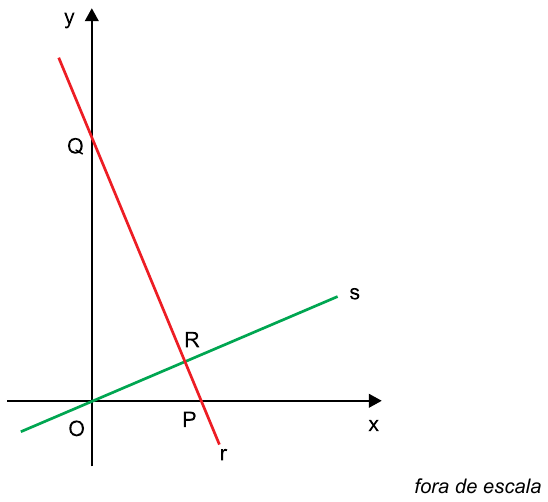
Sabendo que a área do triângulo OPR é igual a 1/5 da área do triângulo OPQ, o coeficiente angular da reta s é igual a
(A) 7/9
(B) 1/3
(C) 5/8
(D) 4/7
(E) 4/5

O objetivo desta questão é encontrar o coeficiente angular da reta s. A estratégia será usar a relação entre as áreas dos triângulos OPR e OPQ para descobrir as coordenadas do ponto R e, com isso, calcular a inclinação da reta s.

O plano de ataque é o seguinte:

• Usar a Relação de Área para Encontrar a Altura: O enunciado diz que a área do triângulo OPR é 1/5 da área do triângulo OPQ. Como ambos os triângulos compartilham a mesma base (o segmento OP), a relação entre suas áreas é diretamente proporcional à relação entre suas alturas. Primeiro, encontramos a altura do triângulo maior (OPQ), que é o ponto onde a reta r corta o eixo Y. Com essa altura, calculamos a altura do triângulo menor (OPR), que corresponde à coordenada Y do ponto R.
• Encontrar a Coordenada X do Ponto R: Agora que sabemos a coordenada Y do ponto R, podemos usar a equação da reta r (na qual o ponto R também se encontra) para descobrir a coordenada X correspondente.
• Calcular o Coeficiente Angular de s: A reta s passa pela origem (0,0) e pelo ponto R, cujas coordenadas acabamos de encontrar. Usando a fórmula do coeficiente angular (m = Δy / Δx), podemos calcular a inclinação da reta s.

Assista ao vídeo acima para ver a aplicação da relação de áreas, os cálculos para encontrar as coordenadas do ponto R e a determinação final do coeficiente angular.

📘 Quer ver mais questões como esta resolvidas em vídeo?
Na Apostila gratuita de Matemática para Vestibulares você encontra esta e muitas outras questões organizadas por prova, com links para as resoluções em vídeo.