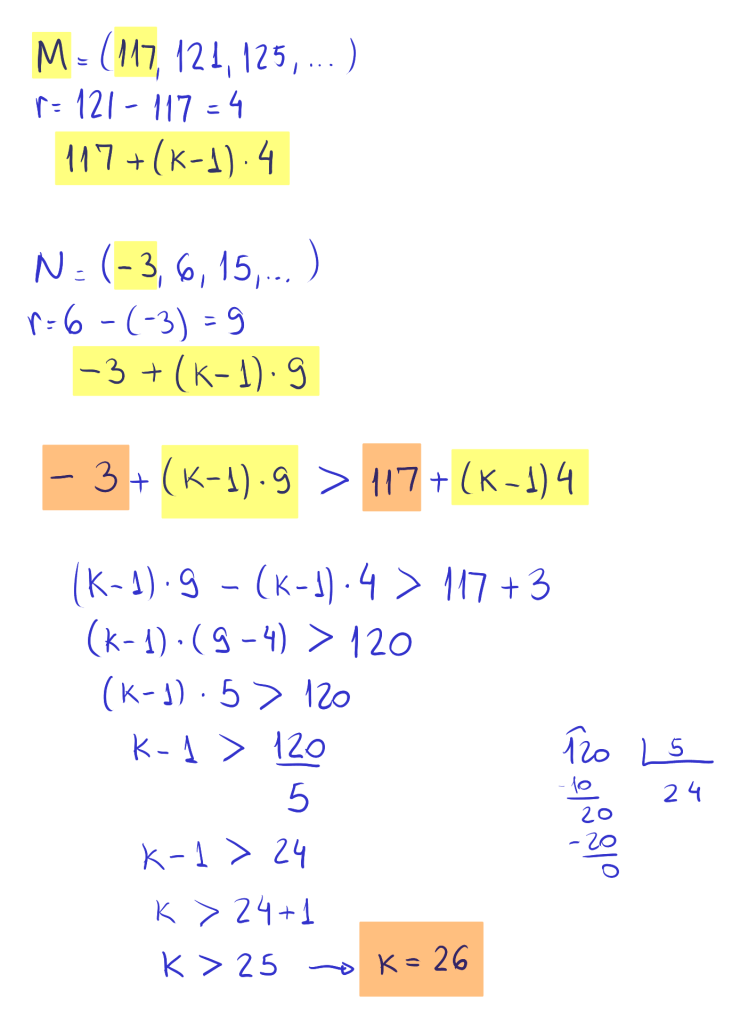Sírio Libanês 2025 – Questão de Progressão Aritmética Resolvida

Uma sequência S é formada pelos elementos das seguintes progressões aritméticas:

A = (-12, -9, -6, -3, 0, 3, 6, 9, 12, …)

B = (115, 117, 119, 121, 123, 125, …)

Os elementos dessas sequências são inseridos em S na ordem em que ocorrem nas progressões e de maneira que, para cada 3 elementos de A, são inseridos 2 elementos de B.

S = (-12, -9, -6, 115, 117, -3, 0, 3, 119, 121, 6, 9, 12, 123, 125, …)

Os elementos de S que estão em posições múltiplas de 5 podem ser representados por s_5k, com k ≥ 1. Observe que:

• Para k = 1, tem-se s_5k = s₅ = 117, que é maior do que s₆ = -3;
• Para k = 2, tem-se s_5k = s₁₀ = 121, que é maior do que s₁₁ = 6.

O menor valor de k para o qual s_5k é menor do que seu sucessor s_5k+1 é:
(A) 29.
(B) 35.
(C) 32.
(D) 38.
(E) 26.