Uma pirâmide reta VEFGH tem uma base quadrada de área 648 cm². Sobre as arestas laterais dessa pirâmide estão os pontos A, B, C e D, tais que ABCD é um quadrado de 288 cm² de área e paralelo à base da pirâmide, conforme mostra a figura.

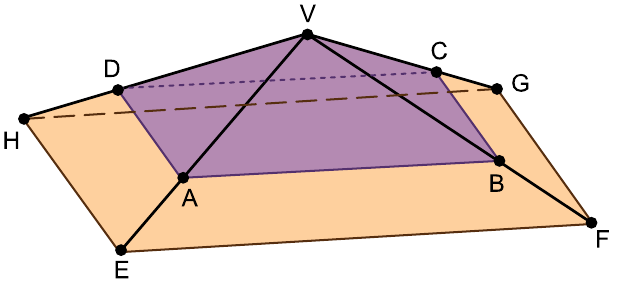
Sabendo que o volume da pirâmide VEFGH excede em 1 140 cm³ o volume da pirâmide VABCD, a medida da aresta VH é igual a
(A) 19,5 cm.
(B) 19,0 cm.
(C) 18,5 cm.
(D) 20,0 cm.
(E) 18,0 cm.

O objetivo desta questão é obter a medida da aresta VH, a estratégia será a seguinte:

• Através da área da base da pirâmide VEFGH, iremos obter a medida (d) da diagonal FH e destacamos que há um triângulo retÂngulo com vértices em V, H e na projeção de V no pont médio da diagonal d.
• Usando razão de semelhança entre áreas K², obteremos a razão de semelhança entre comprimentos K e estabeleceremos uma proporção entre as alturas das pirâmides VEFGH e VABCD.
• Pela fórmula do volume da pirâmide, montaremos uma equação relacionando as duas pirâmides e teremos a altura da pirâmide VEFGH.
• Aplicando o teorema de pitágoras, obtemos a medida de VH.

Assista o vídeo acima e veja o passo a passo da resolução desta questão.

📘 Quer ver mais questões como esta resolvidas em vídeo?
Na Apostila gratuita de Matemática para Vestibulares você encontra esta e muitas outras questões organizadas por prova, com links para as resoluções em vídeo.