Albert Einstein, Vestibular

Albert Einstein 2025 – Questão Resolvida de Matemática: Trigonometria

No plano, as retas r e s são perpendiculares e se cruzam no ponto P, que pertence à circunferência δ. A reta r passa pelo centro O de δ e contém o ponto R de δ. A reta s forma um ângulo de medida θ com o segmento , em que Q é um ponto de δ, como na figura.

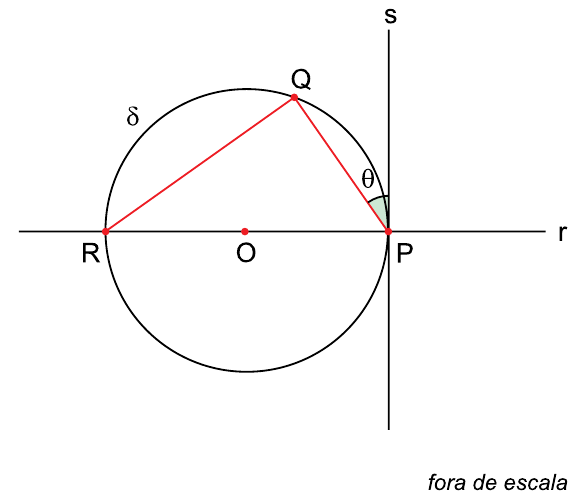
Sabendo que cos θ $= \dfrac{5}{8}$ e que o raio de δ mede 12 cm, a distância entre os pontos R e Q é de

(A) 15 cm

(B) $\dfrac{50}{3}$ cm

(C) $\dfrac{95}{6}$ cm

(D) 16cm

(E) 18 cm

O triângulo $\Delta RQP$ inscrito na circunferência δ é retângulo, pois um de seus lados, $\overline{RP}$ , é o diâmetro de δ.

Conforme a figura

$\angle Q = 90^\circ$
$\angle P = 90^\circ - \theta$
$\angle R = \theta$

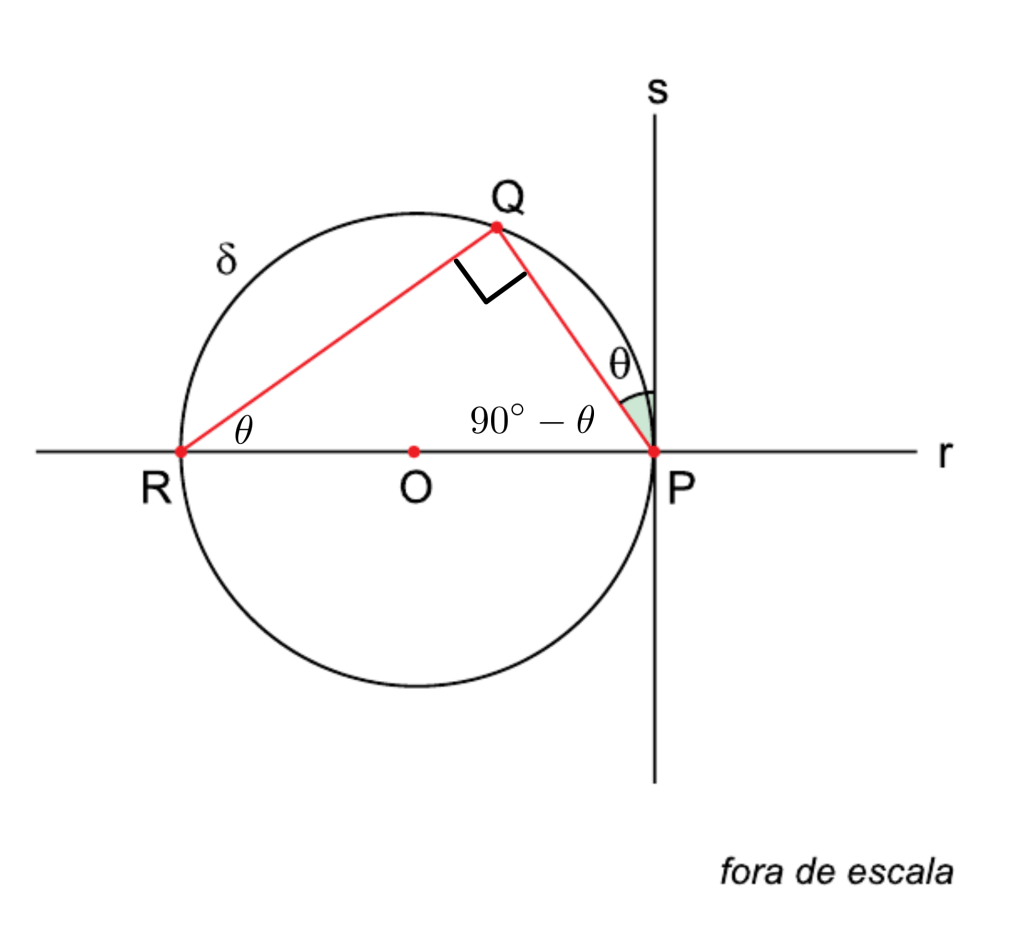
No $\Delta RQP$ a hipotenusa (lado oposto ao ângulo reto) é o diâmetro $\overline{RP}$ , com medida:

$RP = 2 \cdot 12 = 24$

O cateto adjacente a $\angle R$ é o lado $\overline{RQ}$

Usando a relação

$\cos \theta = \dfrac{\text{Cateto Adjacente}}{\text{Hipotenusa}} = \dfrac{RQ}{24}$

Pelo enunciado, $\cos \theta = \dfrac{5}{8}$ . Logo:

$\dfrac{RQ}{24} = \dfrac{5}{8}$

$RQ = \dfrac{24 \cdot 5}{8}$

$RQ = 3 \cdot 5$

$RQ = \boxed{15}$

✅ Resposta correta: (A) 15 cm

Deixe um comentário Cancelar resposta